数论分块
数论分块思想
数论分块可以快速计算一些含有除法向下取整的和式(即形如 $\sum_{i = 1}^{n}f(i)g\lfloor {\frac{n}{i}} \rfloor$的和式)。当可以在 O(1)内计算$f(r) - f(l)$或已经预处理出$f$的前缀和,数论分块就可以在 $O(\sqrt {n})$的时间内计算上述和式的值。
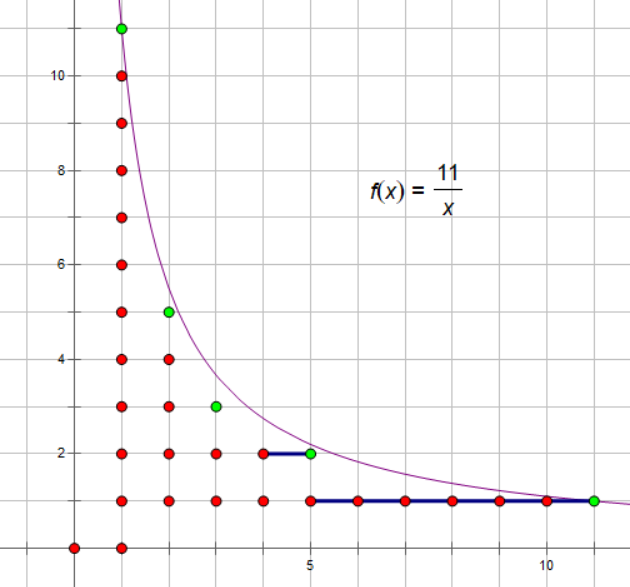
图中共分为了 5 块,这 5 块整点的最大纵坐标都相同。如果统计整点的个数,可以从纵向计数改为横向计数,直接计算 5 个矩形即可。
过程
数论分块的过程大概如下:考虑和式
$\sum_{i=1}^{n}f(i) \lfloor {\frac{n}{i}} \rfloor$
那么由于我们可以知道$\lfloor {\frac{n}{i}} \rfloor$的值成一个块状分布(就是同样的值都聚集在连续的块中),那么就可以用数论分块加速计算,降低时间复杂度。
伪代码如下:
- 获取$f(i)$函数的前缀和, 记为$s(i)$;
- l <– 1
- r <– 0
- result <– 0
- while(l <= n) do :
- r <– $\lfloor {\frac {n}{\frac {n}{i}}} \rfloor$
- result <– result + [s(r) - s(l - 1)] * $\lfloor {\frac {n}{l}} \rfloor$
- l <– r + 1
- end while
最终得到result所为所求的和。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 free-9D!

