爬树的甲壳虫
爬树的甲壳虫

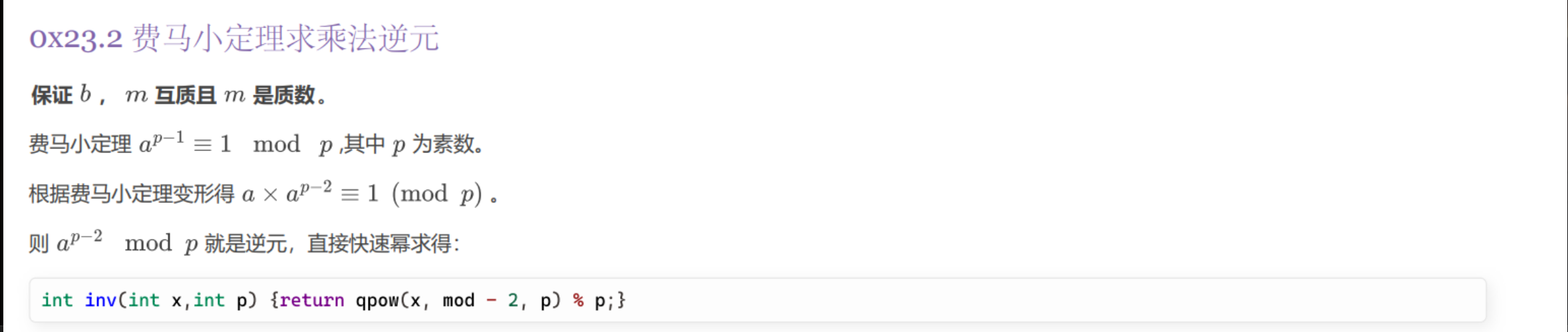
有了以上知识点做铺垫,我们就可以进行如下推导啦!
推导:
根据期望的定义,我们需要先定义两个变量来方便进行数学公式的推导
期望定义:离散型随机变量,期望值就等于将离散变量的每个可能值乘以其概率,然后将所有乘积相加。
因为我们这里是离散型的数据,所以可以用上述定义。

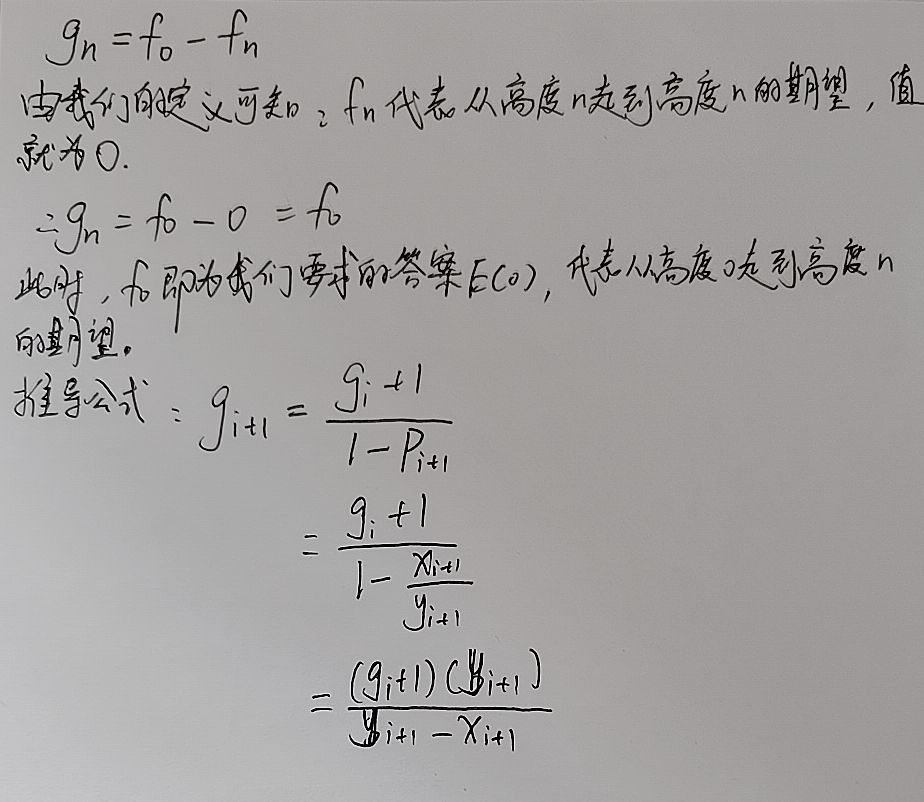
付上我的CODE。
1 | |
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 free-9D!


有了以上知识点做铺垫,我们就可以进行如下推导啦!
根据期望的定义,我们需要先定义两个变量来方便进行数学公式的推导
期望定义:离散型随机变量,期望值就等于将离散变量的每个可能值乘以其概率,然后将所有乘积相加。
因为我们这里是离散型的数据,所以可以用上述定义。

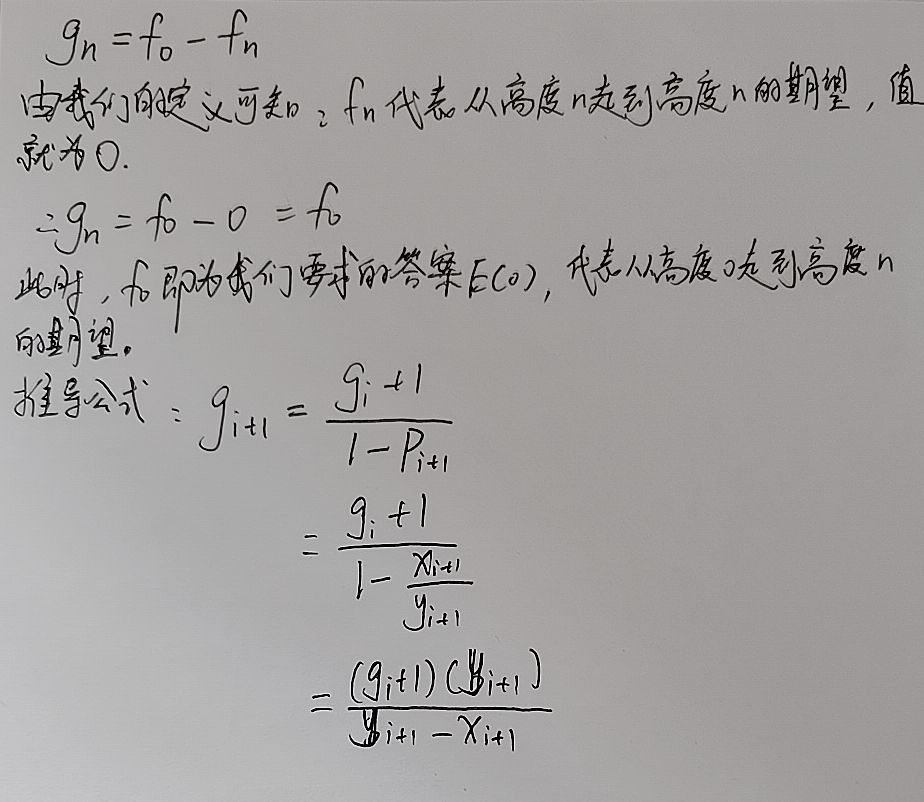
付上我的CODE。
1 | |