超级胶水

题目请点开标题链接进行读题。

读完题，我们很容易想到区间DP来做这道题，但是仔细一看这数据范围，立马就放弃了，因为实在是太大了。

然后大脑搜索log级别的解决思路，发现没有对上号的，放弃。看标签发现是推公式，我瞬间就蒙了，这怎么就能推公式了，看了Y总讲解后，发现思路真的妙啊，下面就来讲讲我自己对Y总思路的理解，有什么不对的，还请大佬指出更正。

对于合并操作，不难理解就是最后一步一定是左区间与右区间合并。例如，我们设中间的点为mid

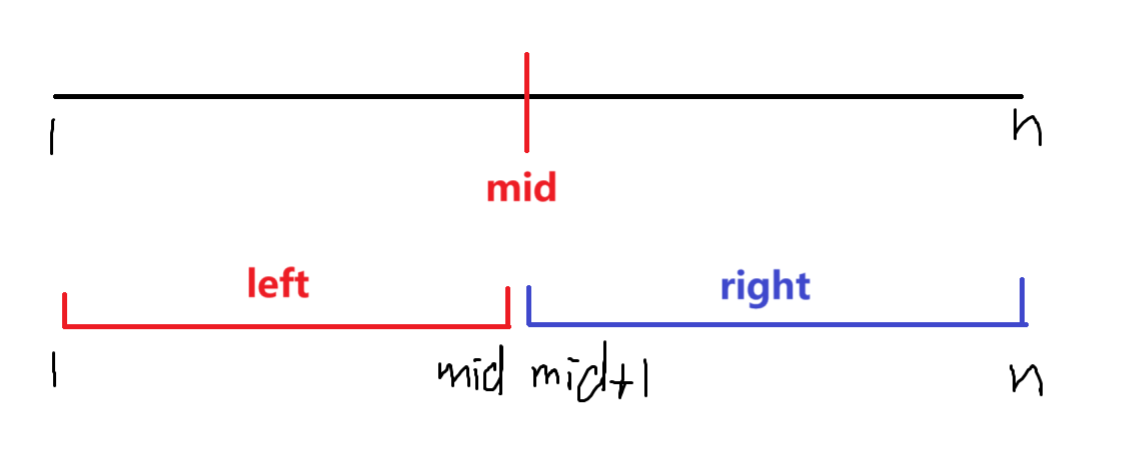
如上图，仔细看，可以发现左区间和右区间其实就是一个规模变小条件不变的子问题，由此我们可以就可以用分治的思路，

中间点其实可以任选，但是题目要求答案最小，这就另人头大，所以我们就猜想中间点的选择不会影响结果，正餐上桌了！

假设有一组数array = [a, b, c, d, e, f, g, h, i, j, k]， 结果 = 左边两两合并 + 右边两两合并 + 左右两边合并

这种操作画个树图就非常容易理解了。

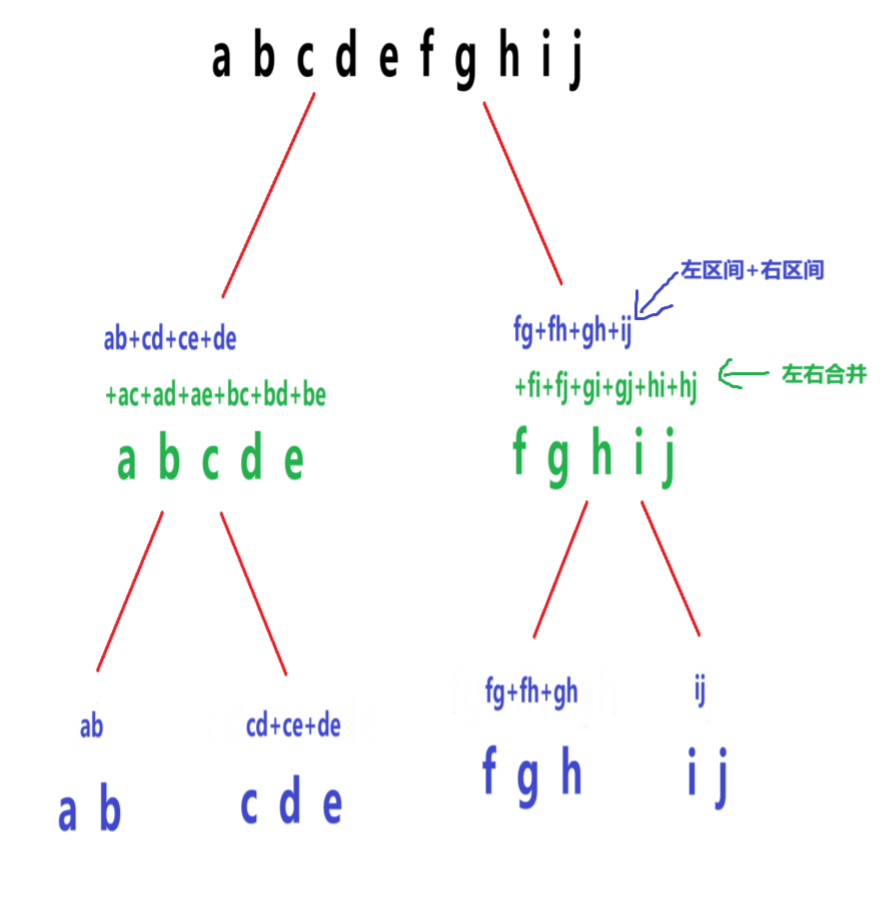
上面是合并结果，下面是分解后的数列，化简一下式子就可以发现经过三步走后，其实等于将数列里面的数两两组合，这样问题就解决了，子问题和主问题其实是一样的，所以答案就是数组中的数两两的乘积相加。

#include <iostream>
#include <algorithm>
using namespace std;

using namespace std;

typedef long long LL;

int n;

int main()
{
    cin >> n;
    LL pre = 0, res = 0;
    for(int i = 1; i <= n; i ++)
    {
        int x; cin >> x;
        res += pre * x;
        pre += x;
    }
    cout << res;
}